JAK SE MĚŘÍ VZDÁLENOSTI VE VESMÍRU?
ČÁST 2 - HVĚZDY A GALAXIE
Blízké hvězdy
To, že i ti největší chytráci se občas mohou mýlit, si ukážeme na příkladu starověkých Řeků. Ti sice dokázali (otázku přesnosti jejich odhadů nechme stranou) přeměřit velikosti i vzdálenosti Země, Měsíce i Slunce, ale v jedné věci se mýlili. Považovali totiž vesmír za geocentrický – podle jejich názoru byla s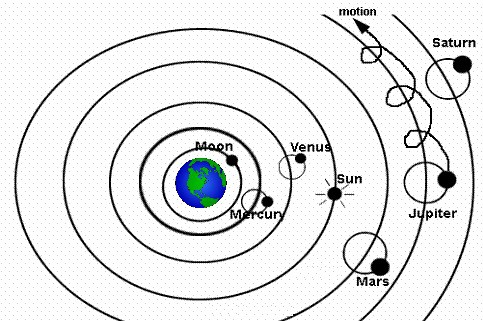 tředem vesmíru Země. Důvodů pro to měli několik: Při pohledu na oblohu vše obíhá kolem Země, všechny předměty padají směrem k Zemi a také necítíme žádný pohyb, protože Země jakožto centrum vesmíru je stále na jednom místě. Navíc kdyby se Země pohybovala, cítili bychom nějaký vítr a měnila by se i paralaxa hvězd, kterou ovšem nikdo nikdy nezaznamenal.
tředem vesmíru Země. Důvodů pro to měli několik: Při pohledu na oblohu vše obíhá kolem Země, všechny předměty padají směrem k Zemi a také necítíme žádný pohyb, protože Země jakožto centrum vesmíru je stále na jednom místě. Navíc kdyby se Země pohybovala, cítili bychom nějaký vítr a měnila by se i paralaxa hvězd, kterou ovšem nikdo nikdy nezaznamenal.
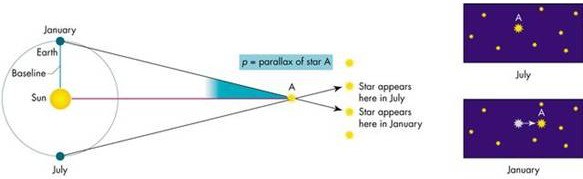
O paralaxe už byla nepatrná zmínka v předchozí kapitole, ale teprve teď bude hrát klíčovou roli. Pojem paralaxa označuje zdánlivý pohyb tělesa vůči vzdálenějšímu pozadí. To se dá velmi snadno demonstrovat, když před sebe natáhnete paži, vztyčíte palec a budete střídavě mrkat levým a pravým okem. Když je levé oko zavřené, vidíte palec v určité poloze, když pravé oko zavřete a otevřete levé, palec jakoby změnil svou polohu vůči druhému konci místnosti a posunul se o kousek doleva. Těch pár centimetrů, které dělí vaše oči, lze využít k přibližnému odhadu vzdálenosti. Pokud ale budete pozorovat hvězdy, žádnou změnu polohy rozhodně nezaznamenáte. Nezaznamenáte jí ani když se budete dívat ze dvou různých míst na Zemi, která jsou od sebe vzdáleny třeba tisícovky kilometrů. Ale co když místo zemského povrchu zvolíte jako základnu oběžnou dráhu Země? Ke Slunci to máme skoro 150 miliónů kilometrů, takže pokud provedeme dvě měření v rozmezí šesti měsíců, pak výsledná základna bude měřit téměř 300 miliónů kilometrů, a to už je pořádně velký měřící nástroj! Nebo ne? Pokud je tato teorie správná, pak by se některé hvězdy, jako třeba hvězda A na následujícím obrázku, měly během půl roku o kousek posunout.
Staří Řekové (a desítky dalších generací) sledovali noční oblohu, ale ani u jedné hvězdy žádnou změnu polohy nezaznamenali. To je jen utvrzovalo v přesvědčení, že Země spočívá bez hnutí na jednom místě, protože pokud by se pohybovala, tak by se i měnila zdánlivá poloha některých hvězd. Musely uběhnout stovky let, aby se od tohoto modelu upustilo. Jeden z mála Řeků, který věřil, že středem vesmíru je Slunce, 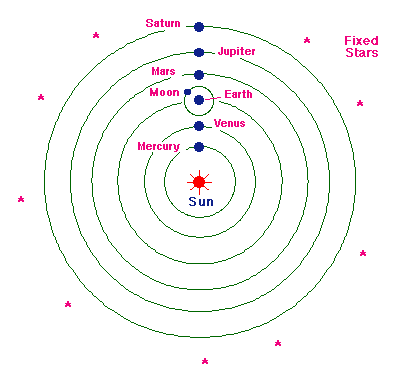 byl náš starý známý Aristarchos. Tvrdil, že kolem něj obíhá Země i další planety a dokonce pobouřil tehdejší svět, když prohlásil, že vesmír je nekonečný, a že naše Slunce není jediné. Byl prohlášen za kacíře (stejně jako většina jeho následovníků) a jeho práce byly zapomenuty. V 16. století oživil myšlenku heliocentrismu Mikuláš Koperník a v následujících dvou stoletích se k němu přidali Galileo Galilei, Johannes Kepler a Isaac Newton. Galileův princip relativity vysvětlil, proč necítíme žádný vítr při pohybu Země kolem Slunce (protože lidé i vzduch se vůči Zemi pohybují stejnou rychlostí), Newton popsal gravitaci (dva předměty se navzájem přitahují, proto jablko padá směrem do středu Země, ale stejně tak je i Země přitahována směrem k jablku, samozřejmě téměř nepostřehnutelně, a ze stejného důvodu i Země obíhá kolem Slunce) a Kepler dokázal předpovědět oběžné dráhy planet. To sice dokázal i geocentrismus, ale za cenu toho, že všechny planetární dráhy byly počítány na základě všelijakých elips, kružnic, kružnic na kružnicích a dalších složitých šílenostech, které se zjevně upravovaly jen proto, aby výpočty souhlasily s pozorováním. Rozhodnutí, která ze dvou teorií popisujících pohyb planet, je správná, může ulehčit tzv. Occamova břitva. Occamova břitva je myšlenkový postup, který říká, že pro vysvětlení určitého jevu či situace by nemělo být použito více argumentů, než je nezbytně nutné. To si můžeme vyložit tak, že pokud máme několik různých vysvětlení vedoucích ke stejnému výsledku, pak je nejspíš správné to nejjednodušší řešení. Příklad: máte narozeniny a dostanete dort. Něco sníte a zbytek, třeba tři kousky, dáte do ledničky. Když večer otevřete ledničku, zjistíte, že jeden kousek chybí. Víte, že doma máte sestru, která miluje sladké, a také máte psa, který dortem pravděpodobně také nepohrdne. Napadají vás dvě možnosti – buďto se pes postavil na zadní, otevřel si ledničku, a zblajznul dort, anebo ho snědla vaše sestra. Pravděpodobnější varianta samozřejmě zavání sestrou. Stejně tak je i Keplerův model na první pohled mnohem jednodušší, a tudíž zřejmě i správný. V 17. a 18. byl geocentrismus definitivně nahrazen heliocentrismem. To už jsme měli poměrně slušnou představu o velikosti naší Sluneční soustavy, ale o vzdálenostech, které panují ve vesmíru, jsme neměli ani potuchy. První, kdo „přiložil pravítko ke hvězdám“, byl německý astronom a matematik Friedrich Bessel.
byl náš starý známý Aristarchos. Tvrdil, že kolem něj obíhá Země i další planety a dokonce pobouřil tehdejší svět, když prohlásil, že vesmír je nekonečný, a že naše Slunce není jediné. Byl prohlášen za kacíře (stejně jako většina jeho následovníků) a jeho práce byly zapomenuty. V 16. století oživil myšlenku heliocentrismu Mikuláš Koperník a v následujících dvou stoletích se k němu přidali Galileo Galilei, Johannes Kepler a Isaac Newton. Galileův princip relativity vysvětlil, proč necítíme žádný vítr při pohybu Země kolem Slunce (protože lidé i vzduch se vůči Zemi pohybují stejnou rychlostí), Newton popsal gravitaci (dva předměty se navzájem přitahují, proto jablko padá směrem do středu Země, ale stejně tak je i Země přitahována směrem k jablku, samozřejmě téměř nepostřehnutelně, a ze stejného důvodu i Země obíhá kolem Slunce) a Kepler dokázal předpovědět oběžné dráhy planet. To sice dokázal i geocentrismus, ale za cenu toho, že všechny planetární dráhy byly počítány na základě všelijakých elips, kružnic, kružnic na kružnicích a dalších složitých šílenostech, které se zjevně upravovaly jen proto, aby výpočty souhlasily s pozorováním. Rozhodnutí, která ze dvou teorií popisujících pohyb planet, je správná, může ulehčit tzv. Occamova břitva. Occamova břitva je myšlenkový postup, který říká, že pro vysvětlení určitého jevu či situace by nemělo být použito více argumentů, než je nezbytně nutné. To si můžeme vyložit tak, že pokud máme několik různých vysvětlení vedoucích ke stejnému výsledku, pak je nejspíš správné to nejjednodušší řešení. Příklad: máte narozeniny a dostanete dort. Něco sníte a zbytek, třeba tři kousky, dáte do ledničky. Když večer otevřete ledničku, zjistíte, že jeden kousek chybí. Víte, že doma máte sestru, která miluje sladké, a také máte psa, který dortem pravděpodobně také nepohrdne. Napadají vás dvě možnosti – buďto se pes postavil na zadní, otevřel si ledničku, a zblajznul dort, anebo ho snědla vaše sestra. Pravděpodobnější varianta samozřejmě zavání sestrou. Stejně tak je i Keplerův model na první pohled mnohem jednodušší, a tudíž zřejmě i správný. V 17. a 18. byl geocentrismus definitivně nahrazen heliocentrismem. To už jsme měli poměrně slušnou představu o velikosti naší Sluneční soustavy, ale o vzdálenostech, které panují ve vesmíru, jsme neměli ani potuchy. První, kdo „přiložil pravítko ke hvězdám“, byl německý astronom a matematik Friedrich Bessel.
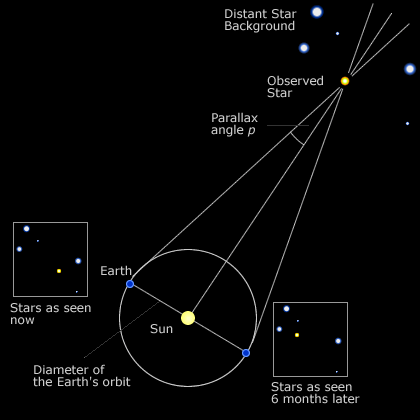
Do té doby se nikomu nepodařilo změřit hvězdnou paralaxu, a tak se všeobecně soudilo, že hvězdy musí být „neuvěřitelně daleko.“ Jejich paralaxa tedy musí být tak „neskutečně mrňavá“, že ji nelze změřit. Besselovi se to ale roku 1838 podařilo. V rozmezí šesti měsíců změřil paralaxu hvězdy 61 Cygni a prohlásil, že se za tu dobu posunula o úhel 0,0001742° (to je 0,62712 úhlové vteřiny). Ostrý úhel v pravoúhlém trojúhelníku tak měřil 0,0000871°. To je stejné jako kdybyste ze vzdálenosti 6,5 km pozorovali malým dalekohledem svíčku, kterou někdo posunul o jeden centimetr! Jestliže podělíme délku základy (to jest vzdálenost Země-Slunce) tímto úhlem, dostaneme vzdálenost 61 Cygni: 149,6·106 / tan0,0000871 = 98,4 biliónů km. Jeho odhad tak zněl, že hvězda je od nás vzdálena 10,4 světelných let (dnešní správný údaj je 11,4). To se může zdát jako obrovská vzdálenost, ale na vesmírná měřítka je něco jako náš blízký soused.


Například Polárka má paralaxu 0,00756´´. Nachází se tedy od nás ve vzdálenosti 431 světelných let [149,6·106 / (tan0,00756/3600) = 4,1 biliardy km = 431 světelných let]. Naše nejbližší hvězda (kromě Slunce samozřejmě), Proxima Centauri, má paralaxu 0,77233" a je od nás vzdálena 4,2 světelného roku.
Paralaxa je sice poměrně přesná metoda určování vzdálenosti hvězd, ale už jen z její podstaty vyplývá nevyhnutelný závěr, že s ní můžeme měřit jen ty nejbližší hvězdy, neboť čím vzdálenější hvězdu pozorujeme, tím je její paralaxa menší, a tudíž i hůře měřitelná. Pokud měříme ze Země, paralaxu lze úspěšně využít na vzdálenosti v řádu několika málo stovek světelných let. Vesmírná sonda Hipparcos (zkratka z High Precision Parallax Collecting Satellite), která byla vypuštěna v roce 1989 s účelem měřit hvězdné paralaxy, dokázala s přesností na 0,001" změřit paralaxu skoro u 120 000 hvězd na vzdálenost až 1600 světelných let a výrazně nám tak pomohla zpřesnit kosmická měřítka. S o něco menší přesností (0,01") pak zmapovala i dalších dva a půl milionu hvězd.
Naše Galaxie
Malá poznámka, kterou klidně můžete...
Než se pustíme do dalšího povídání, ujasněme si, co si vlastně představujeme pod pojmem "naše Galaxie". Jak jste si asi všimli, pak ve slově Galaxie píši velké G. Je to z toho důvodu, že v češtině je její oficiální název prostě jen "Galaxie" a nic víc. Pokud byste ale o ní četli v různých jazycích, pak byste zjistili, že se jí většinou neřekne jinak než "Mléčná dráha". V češtině ale tento pojem neoznačuje celou galaxii, nýbrž jen její určitou část - konkrétně je to stříbřitý pás táhnoucí se noční oblohou. Ve skutečnosti je tedy Mléčná dráha jen malou částí naší Galaxie. Ze Země je tak dobře viditelná proto, že je tvořena hvězdami, které se nalézají ve směru hlavní roviny disku Galaxie (je to zkrátka jako kdybyste se dívali na hranu mince). To, co však vidíme, není její centrum, ale pouze dvě její spirální ramena. Obyčejným okem střed naší Galaxie neuvidíte, neboť vám ho blokují právě ony dvě zmíněná ramena. Ty obsahují takovou koncentraci hvězd, že nám při pohledu ze Země splývají do jednoho zdánlivě spojitého útvaru – je to zkrátka takový obláček připomínající rozlité mléko, odtud také název Mléčná dráha. Tento pojem ale tak zlidověl, že když někdo mluví o Mléčné dráze, má většinou na mysli celou Galaxii. Proto, aby se vyvrátily jakékoliv pochybnosti, se občas používá i termín „Galaxie Mléčná dráha“ – tak či tak, už by si v tom astronomové měli konečně udělat jasno!
...přeskočit 
Na změření vzdálenějších hvězd už nám hvězdná paralaxa stačit nebude. S určením vzdáleností hvězd v rámci naší Galaxie, která napříč měří kolem 100 000 světelných let, nám pomůže tzv. Hertzsprung-Russelův diagram. Ten zachycuje závislost mezi zářivým výkonem hvězdy (svítivostí) a její povrchovou teplotou.
Povrchovou teplotu Slunce jsme si spočetli již v předchozí kapitole. Vyšla nám 5800 K a jediné, co jsme k tomu potřebovali, bylo znát vlnovou délku maxima jeho vyzařování. Různá povrchová teplota znamená různou vlnovou délku. Čím je vlnová délka kratší, tím je hvězda teplejší. Vlnová délka, kterou pozorujeme, a tedy i teplota, souvisí s barvou hvězdy. Obecně platí, že nejchladnější hvězdy jsou červené a oranžové. O něco teplejší hvězdy, jako například naše Slunce, jsou žluté a žlutobílé. Nejteplejší hvězdy pak září barvami od bílé až po modrou.
Barvu hvězdy zjišťujeme spektrální analýzou. Tou můžeme určit nejenom chemické složení hvězdy, ale i rychlost jejího pohybu a především její teplotu. Spektrálních tříd je vícero druhů, v následujícím textu se budeme zabývat pouze Harvardskou klasifikací. Ta dělí hvězdy podle povrchové teploty od nejžhavějších po nejchladnější dle následujícího posloupnosti: (Q – P – W) – O – B – A – F – G – K – M – (L – C – S). Písmena v závorkách se vyskytují jen výjimečně, a to z důvodu jemnějšího rozdělení. Občas se k písmenům ještě přidávají čísla 0 až 9, ale nám bohatě postačí klasická stupnice OBAFGKM. Jako mnemotechnickou pomůcku si můžete zapamatovat "Oh, Be A Fine Girl/Guy, Kiss My Lips" nebo český ekvivalent "Olda bude asi fňukat, Gustave, kup mu lízátko".
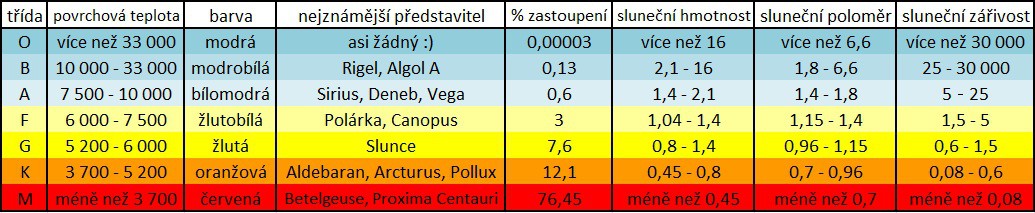
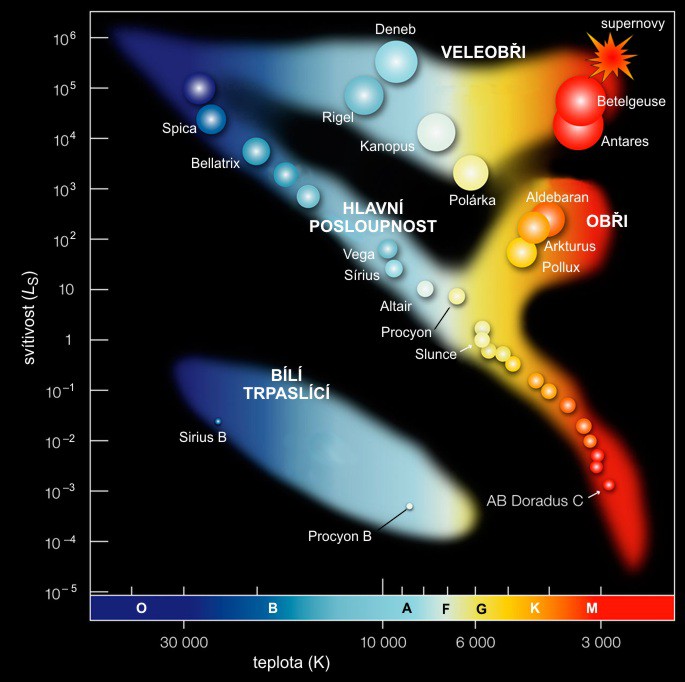
K výše uvedené tabulce se sluší dodat, že teplota je v Kelvinech, a že všechny hodnoty vztažené k Slunci (hmotnost, poloměr a zářivost) platí pouze pro hvězdy na hlavní posloupnosti. Co je ta hlavní posloupnost, je zřejmé z následujícího obrázku. Je to pás, který se táhne napříč celým H-R diagramem z levého horního rohu až po pravý dolní roh, a vyskytuje se na něm asi 90% všech hvězd. Můžeme si všimnout, že hvězdy jsou rozloženy nerovnoměrně - mimo hlavní posloupnost se nachází tři skupiny hvězd (ve skutečnosti jich je mnohem více, ale toto jsou ty nejdůležitější). Vlevo dole jsou trpaslíci a vpravo nahoře jsou obři a veleobři. Při výpočtu svítivosti Slunce jsme zjistili, že svítivost je přímo závislá na povrchové teplotě a na poloměru hvězdy. Pokud tedy známe svítivost nějaké hvězdy, můžeme pomocí H-R diagramu spočítat i její poloměr. Hvězdy ležící nad sebou mají stejnou teplotu, ale hvězdy, které leží výš, mají větší svítivost než hvězdy na hlavní posloupnosti. Níže položené hvězdy zase mají svítivost nižší. Například Sirius A (nejjasnější hvězda noční oblohy) leží na hlavní posloupnosti a má téměř stejnou povrchovou teplotu (skoro 10 000 Kelvinů) jako Deneb, který leží mimo ni. To znamená, že Deneb musí mít mnohem větší poloměr, a tudíž i zářivost. (Sirius je 1,7x větší než Slunce a má zářivost 25 Sluncí, zatímco Deneb je asi dvěstěkrát větší než Slunce a jeho zářivost dosahuje kolem 200 000 Sluncí.)
Nyní nastal čas na trochu nudnou, ale velmi důležitou vsuvku. Hvězdná terminologie je poměrně ošemetná věc, nicméně je nutné se zmínit alespoň o třech důležitých veličinách, které se často nesprávně zaměňují. Nejprve je třeba si uvědomit rozdíl mezi pojmy zářivost a jasnost. Zářivost (jinak též zářivý výkon nebo také svítivost) je celkové množství energie, kterou hvězda vyzáří do prostoru za jednotku času, zatímco jasnost (zdánlivá jasnost nebo zdánlivá magnituda) nám jen říká, jak moc jasně se nám jeví na obloze. Jasnost je tedy subjektivní pojem, který se skutečnou zářivostí nemá příliš společného, neboť závisí především na vzdálenosti. Pak máme také absolutní jasnost (=absolutní magnituda či absolutní hvězdná velikost), což je jasnost, kterou by hvězda měla, kdybychom se na ni dívali ze vzdálenosti 10 parseků. (Jeden parsek je jedna ze tří nejdůležitějších astronomických jednotek a rovná se vzdálenosti 3,26 světelného roku. Myslím, že není důležité tu rozebírat, jak tato jednotka vznikla, a proč má zrovna tuto hodnotu, ale asi nebude na škodu se aspoň zmínit o tom, že se používá především v odborných článcích, zatímco v populárně naučné literatuře se pro vyjadřování vzdáleností využívají nám dobře známé světelné roky. Pokud by vás zajímalo, jaká je ta třetí astronomická jednotka, tak její název vás možná trošku zaskočí, protože se jí říká prostě "Astronomická jednotka". Označuje se AU a její velikost si můžeme nejjednodušeji ředstavit jako střední vzdálenost mezí Zemí a Sluncem.)
Byli to opět staří Řekové, kdo jako první rozdělil hvězdy podle jasnosti. Tehdejší stupnice měla 6 tříd – v té první se nacházely nejjasnější hvězdy na obloze, ve druhé o něco slabší, a v té poslední, šesté, byste takovou hvězdu už jen sotva zahlédli. Nebylo to zrovna přesné hodnocení, protože se provádělo tak, že jste se prostě koukli na oblohu a určili jste, která hvězda se vám zdá jasnější.

Podobnou stupnici používáme i v dnešní době, ovšem s tím rozdílem, že je přesně matematicky definovaná a její jednotkou je magnituda. Magnituda tedy vyjadřuje jasnost objektů na obloze a se svým starořeckým předchůdcem má společné snad jen to, že čím nižší číslo má, tím jasnější objekt popisuje. Možná to bude znít zvláštně, ale magnituda může nabývat jak kladných, tak záporných hodnot. Například nejjasnější objekt na obloze, Slunce, má magnitudu -26,7. Měsíc v úplňku má -12,6 magnitudy, nejjasnější hvězda noční oblohy, Sírius, má -1,5 magnitudy a třeba taková Polárka má magnitudu +2. (Znaménko plus se tam obvykle nepíše, dal jsem ho tam jen pro názornost.) V městské zástavbě je možné prostým okem zahlédnout objekty s magnitudou nižší než 3 nebo 4. Pokud víte kam se koukat, pak za vhodných podmínek můžete zahlédnout i hvězdy s magnitudou 5 až 6. Jestli se nacházíte na dobrém místě, máte oči adaptované na tmu, a navíc ještě k tomu orlí zrak, tak i 6,5. Na vyšší magnitudy již budete potřebovat dalekohled. Nejvzdálenější objekty (tedy alespoň ty, které jsou pozorovatelné viditelným světlem) pak můžete zahlédnout Hubbleovo vesmírným dalekohledem, a to až do magnitudy 30. (Když to shrneme do nějakých rozumných čísel, tak prostým okem lze ze Země spatřit asi kolem 9 - 12 tisíc hvězd. Toto číslo navíc musíme podělit dvěmi, protože na opačné polokouli mají den. Za bezměsíčné noci a dalších příznivých okolností tedy můžeme najednou spatřit asi 5 000 hvězd. Pokud uvážíme naše zeměpisné podmínky, tak se ve většině případů budeme muset spokojit jen s pár stovkami.) Další zvláštností magnitudy je, že se nemění lineárně, ale logaritmicky. Rozdíl mezi jednou třídou magnitudy je v poměru jasnosti 2,5. To znamená, že hvězda první magnitudy je 2,5x jasnější než hvězda druhé magnitudy. Vzájemný poměr jasnosti v rozdílu pěti magnitud je tak 1:100 (2,55 = cca 100). Nyní se tak dostáváme k vysvětlení, proč má Slunce magnitudu zrovna -26,7. V zájmu zachování stupnice čím menší číslo, tím větší jasnost, bylo zvoleno, že pro všechna měření budeme vycházet z hvězdy zvané Vega. Cokoliv jasnější než Vega bude mít zápornou magnitudu, cokoliv tmavšího pak zase kladnou – to znamená, že jasnost Vegy je nula (tato hodnota byla později upravena na 0,03, ale na principu to nic nemění). Jelikož Slunce je 50 miliardkrát jasnější než Vega, pak jeho magnituda je -2,5 log (50 000 000 000), což je právě oněch zmíněných -26,7.
Absolutní magnitudu Slunce pak spočteme podle vzorce {zdánlivá magnituda – 5 [(log vzdálenosti hvězdy v parsecích) – 1]}, po dosazení nám tedy vyjde, že Slunce má absolutní magnitudu skoro pět. { -26,7 – 5 [(log 4,864·10-6) – 1]} = 4,9.
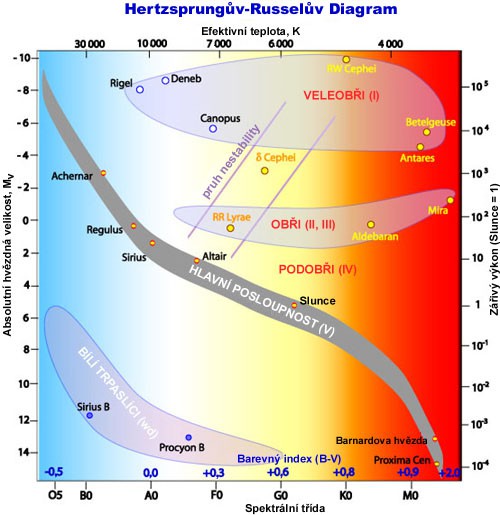
Protože zářivost neboli svítivost je přímo závislá na absolutní magnitudě, často se z praktických důvodů vyskytuje H-R diagram, který má na jedné svislé ose absolutní magnitudu, a na druhé ose zářivost.
Pro zjišťování vzdáleností pak můžeme vycházet ze známého faktu, že intenzita záření klesá s druhou mocninou vzdálenosti. Pokud pozorujete dvě hvězdy, a obě se vám zdají být stejně jasné, pak to znamená, že buďto mají obě stejnou zářivost a nachází se od vás stejně daleko, anebo (a to je mnohem pravděpodobnější) se jedna z nich nachází dál, ale je více zářivá.
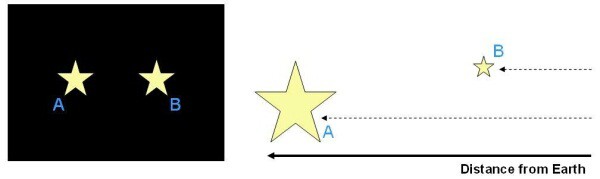
Z toho také vyplývá, že pokud najdete dvě hvězdy o stejné zářivosti, ale jedna z nich bude devětkrát jasnější než druhá, pak se ta druhá musí nacházet ve trojnásobné vzdálenosti, protože odmocnina z devíti jsou tři. První H-R diagram tedy vznikl tak, že se vzaly všechny hvězdy, u nichž byla známa jejich vzdálenost (ta se určila pomocí hvězdné paralaxy), povrchová teplota i jasnost, a tím se zjistila i zářivost. Vztah mezi barevným spektrem hvězdy a její zářivostí nevznikl náhodou, ale byl spočten na vzorku několika tisíců hvězd. K určení vzdálenosti hvězdy nám tak v podstatě stačí jen dvě věci: změřit její jasnost a zjistit vlnovou délku (barvu), kterou hvězda vyzařuje. Na základě porovnání zdánlivé a skutečné jasnosti pak můžeme zjistit vzdálenost sledované hvězdy. Vzhledem k tomu, že se stále se zvyšující vzdáleností klesá i jasnost hvězd, lze tuto metodu využít jen v rámci naší Galaxie. Na větší vzdálenosti je jas už tak slabý, že hvězdy nemůžeme přesně změřit (navíc jsou "blízko" u sebe, takže není jednoduché zaměřit jednu konkrétní hvězdu), proto je tato metoda použitelná asi do vzdálenosti čtvrt miliónu světelných let.
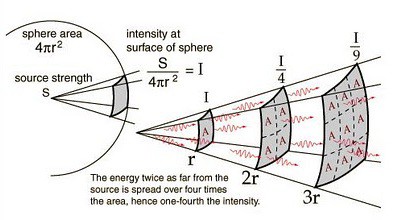
H-R diagram má mnohostranné využití, umí toho daleko víc, než jen zjišťovat vzdálenosti a velikosti hvězd. Můžeme z něj například vyčíst hmotnost hvězd, neboť hmotnost je přímo závislá na zářivosti. [Podle vzorce L/Ls = (M/Ms)n, kde Ls je zářivý výkon Slunce a Ms hmotnost Slunce, člen n pak záleží na konkrétním typu hvězdy.] Jelikož každá hvězda během svého života prochází určitým vývojem, lze na H-R diagramu znázornit i její stav v různých časových fázích - ne nadarmo se tak o něm se říká, že je to nejznámější astronomický diagram.
Blízké galaxie
Se stále se zvyšující vzdáleností klesá i jasnost hvězd. V naší nejbližší galaxii, Andromedě, jsou hvězdy už tak málo jasné, že metodu hlavní posloupnosti už nelze využít, a je třeba zavést metodu jinou. Jednou z nich je pozorování obřích proměnných hvězd zvaných cefeidy. Pokud jste četli kapitolu o Velkém třesku a vývoji hvězd, pak víte, že hvězdy jsou v rovnováze díky dvěma klíčovým silám: gravitaci a tlaku. Gravitace přitahuje veškerou hmotu směrem do středu hvězdy, zatímco termonukleární fúze uvnitř jádra zas vytváří tlak, jenž hvězdu naopak zvětšuje. Cefeidy mají jednu zvláštní vlastnost, a to, že  tyto dvě síly u nich nejsou v rovnováze - hvězda se tak střídavě smršťuje a rozpíná, čímž pravidelně mění svou jasnost. Když je gravitace silnější, hvězda se smršťuje a vydává méně světla, jakmile ale uvnitř začne narůstat tlak, hvězda se nafoukne a opět tak zvýší svou zářivost. Tato pulzace se odehrává v řádu několika dní či měsíců.
tyto dvě síly u nich nejsou v rovnováze - hvězda se tak střídavě smršťuje a rozpíná, čímž pravidelně mění svou jasnost. Když je gravitace silnější, hvězda se smršťuje a vydává méně světla, jakmile ale uvnitř začne narůstat tlak, hvězda se nafoukne a opět tak zvýší svou zářivost. Tato pulzace se odehrává v řádu několika dní či měsíců.
Astronomka Henrietta Leavitt přesně před sto lety pozorovala cefeidy a všimla si závislosti mezi měnící se zdánlivou jasností a dobou periody. Jak taková závislost vypadá u čtyř různých cefeid, si můžete prohlédnout na následujícím obrázku.
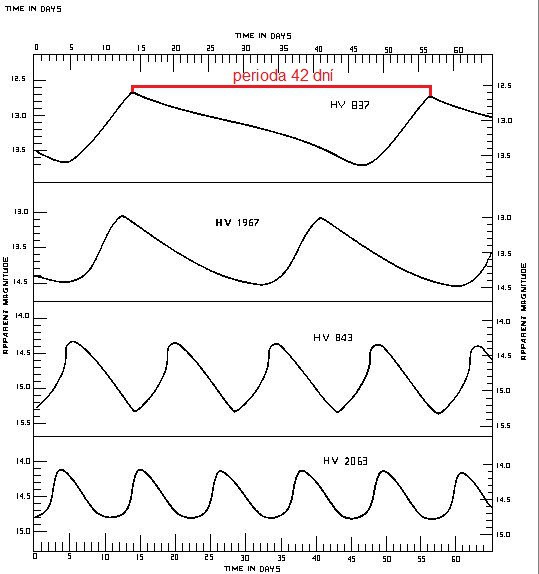
V Malém Magellanovu mračnu (to je trpasličí galaxie, která je s námi gravitačně vázaná a nachází se ve vzdálenosti asi 200 000 světelných let) nalezla Leavitt 25 cefeid, z nichž některé byly jasnější a některé méně jasné. Protože se všechny nacházely pravděpodobně ve stejné vzdálenosti, dospěla k závěru, že jasnější cefeidy se nám jeví jasněji nikoli proto, že by byly blíž, ale proto, že jsou i ve skutečnosti zářivější.
Z této závislosti pak odvodila vztah, podle něhož lze vypočítat absolutní jasnost. Pokud známe dobu periody, pak ji můžeme dosadit do grafu (anebo do vzorce, který naleznete o několik odstavců níž) a určit tak skutečný zářivý výkon hvězdy nebo její absolutní jasnost. Z grafu je patrné, že čím delší má hvězda periodu, tím je i zářivější.
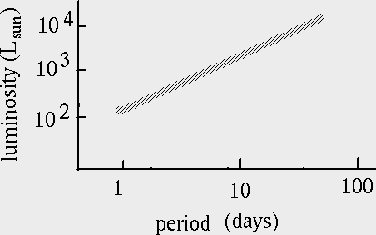
Už dříve jsme si řekli, že intenzita záření klesá s druhou mocninou vzdálenosti. Ovšem co je nám platné vědět, že jedna hvězda se nachází třeba třikrát dál než druhá, když nevíme vzdálenost ani jedné z nich? Stačí „pouze“ zjistit vzdálenost jedné blízké cefeidy a rázem tak můžeme měřit vzdáleností galaxií. Pokud tedy pozorujeme dvě cefeidy a známe vzdálenost té bližší (tu zjistíme například pomocí paralaxy či jiné metody), pak snadno dopočítáme vzdálenost i té vzdálenější. Proto jsou cefeidy označovány jako standardní svíčky nebo jako majáky vesmíru.

Ovšem kde takovou blízkou "kalibrační" cefeidu vzít? V souhvězdí Orla se nachází proměnná hvězda FF Aquilae o jasnosti 5,3 magnitudy. O několik odstavců výš jsme si pomocí paralaxy spočítali vzdálenost Polárky, která má jasnost 2 magnitudy – na noční obloze se nám tedy jeví asi 20x jasněji než FF Aquilae (protože 2,5(5,3 – 2) = 20). Ačkoli to moc lidí neví, naší nebližší cefeidou je právě Polárka. Je to asi nejsnadněji nalezitelná hvězda viditelná ze severní polokoule, protože se za prvé nachází vždy na severu, a za druhé se kolem ní točí celá hvězdná obloha. Okem to samozřejmě nezaznamenáte, ale věřte mi, že má periodu skoro 4 dny. Interval FF  Aquilae je jen o půl dne delší. Z toho vyplývá, že obě hvězdy by měli mít i podobnou zářivost. Jestliže Polárku vidíme 20x jasněji než FF Aquilae, pak se FF Aquilae musí nacházet téměř v pětinásobné vzdálenosti, protože druhá odmocnina z dvaceti je skoro pět. Když vynásobíme nám známou vzdálenost Polárky (asi 433 světelných let) pěti, pak zjistíme, že FF Aquilae je od nás vzdálena nějakých 2000 světelných let.
Aquilae je jen o půl dne delší. Z toho vyplývá, že obě hvězdy by měli mít i podobnou zářivost. Jestliže Polárku vidíme 20x jasněji než FF Aquilae, pak se FF Aquilae musí nacházet téměř v pětinásobné vzdálenosti, protože druhá odmocnina z dvaceti je skoro pět. Když vynásobíme nám známou vzdálenost Polárky (asi 433 světelných let) pěti, pak zjistíme, že FF Aquilae je od nás vzdálena nějakých 2000 světelných let.
Nyní zkusme vypočítat vzdálenost cefeidy HV 837. Z grafu (viz výše) nám vypadlo, že perioda trvá 42 dní a zdánlivá jasnost se pohybuje mezi 12,7 až 13,7 magnituda. Jako střední hodnotu (pozor, neplést s průměrem) budeme brát 13 magnituda. Tuto periodu pak porovnáme s periodou nějaké nám známé cefeidy a zjistíme absolutní jasnost.
V tomto případě je výsledná magnituda něco kolem -5,9 (tu zjistíme podle následujícího grafu anebo podle vzorce -2,81log(délka periody ve dnech) – 1,43, což vychází zhruba na -6). Tu pak dosadíme do vzorečku na fotometrickou paralaxu 10[0,2(mV-MV)+1] a dostaneme číslo 60 tisíc parseků (cca 18,4 tisíc světelných let). (Fotometrická proto, že její vlastnosti byly zjištěny fotometricky.)
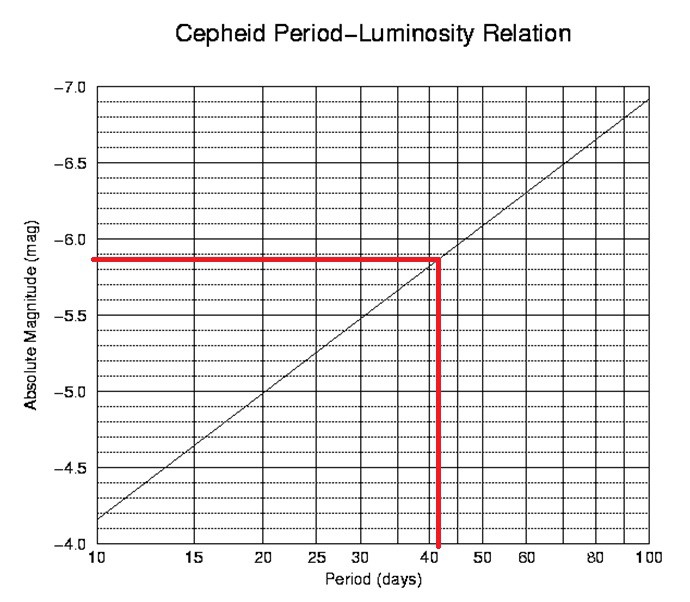
Předchozí příklady jsou trochu zjednodušené, protože před samotným výpočtem je nutno zjistit, o jaký typ proměnné hvězdy se vlastně jedná. (Kdybyste se snažili si ověřit vzdálenosti hvězd jen podle grafů či vzorečků, tak vám stejnak půlka vyjde jinak než je udávaná hodnota. Z toho nic nedělejte – v odhadování vzdáleností hraje roli spousta dalších okolností a navíc fakt, že cefeidy se stejnou periodou mají i stejnou zářivost není ani tak fakt, jako spíše zbožné přání astronomů. To ale neznamená, že by měření vzdáleností pomocí cefeid bylo nepřesné. Reálné výpočty jsou ovlivněny ještě mnoha dalšími faktory, takže cefeidy jsou naopak jedny z nejpřesnějších metod.) Jedna z úplně prvních objevených proměnných hvězd byla Algol. Dlouho se mělo za to, že změna její zdánlivé jasnosti má fyzikální původ, ale později se zjistilo, že se jedná o tzv. zákrytovou hvězdu. To znamená, že Algol má v reálu stále stejnou zářivost, a náhlý pokles jasnosti je způsobem tím, že kolem něj obíhá jiná, menší hvězda, která nám jeho jas pravidelně zastiňuje. Tyto systémy  proměnných hvězd jsou však poměrně snadno rozeznatelné, protože cefeidy se rychle vzepnou k nárůstu jasnosti a pak dlouho pohasínají, zatímco u zákrytových (dvoj)hvězd je nárůst i pokles jasu stejně rychlý. Ve skutečnosti rozlišujeme několik typů proměnných hvězd, pokud vyjmenujeme ty nejdůležitější, pak se jedná o hvězdy typu RR Lyrae a cefeidy první a druhé populace.
proměnných hvězd jsou však poměrně snadno rozeznatelné, protože cefeidy se rychle vzepnou k nárůstu jasnosti a pak dlouho pohasínají, zatímco u zákrytových (dvoj)hvězd je nárůst i pokles jasu stejně rychlý. Ve skutečnosti rozlišujeme několik typů proměnných hvězd, pokud vyjmenujeme ty nejdůležitější, pak se jedná o hvězdy typu RR Lyrae a cefeidy první a druhé populace.
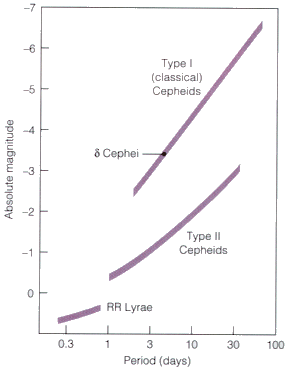 Jak můžete z grafu napravo vyčíst, mezi první a druhou populací cefeid je rozdíl v magnitudě - typy I jsou o 1,5 magnitudy jasnější než cepheidy typu II o stejné periodě (proto, když počítáte magnitudu u cefeid druhého typu, musíte na konci předchozího vzorečku místo čísla -1,43 použít číslo +0,15).
Jak můžete z grafu napravo vyčíst, mezi první a druhou populací cefeid je rozdíl v magnitudě - typy I jsou o 1,5 magnitudy jasnější než cepheidy typu II o stejné periodě (proto, když počítáte magnitudu u cefeid druhého typu, musíte na konci předchozího vzorečku místo čísla -1,43 použít číslo +0,15).
Když Edwin Hubble pozoroval cefeidy v Andromedě, a porovnal je s cefeidami v naší Galaxii, myslel si, že všechny cefeidy mají stejné vlastnosti, a dospěl k názoru, že Andromeda je od nás vzdálena asi 900 000 světelných let. To tehdy ve světě (a nejenom v tom vědním) způsobilo značný poprask, neboť do té doby se mělo za to, že celý vesmír je tvořen jen naší Galaxií. (Ta však měří v průměru asi 100 000 světelných let, a tudíž bylo jasné, že pozorované objekty se nachází daleko za jejími hranicemi - z toho tedy vyplynulo, že vesmír je zřejmě mnohem větší, než se tenkrát myslelo.) Edwin Hubble měl mezi astronomy tak velký respekt, že si nikdo nedovolil zpochybňovat jeho výpočty. (Stejný respekt měl v první polovině 20. století i Arthur Eddington – ten dokonce odrazoval své studenty od toho, aby se zabývali studiem černých děr, neboť se domníval, že něco tak neuvěřitelného prostě nemůže existovat. Expertem na špatné předpovědi byl ale jiný excelentní vědec, fyzik Lord Kelvin. Rentgenové paprsky pokládal za kouzelnický trik (uvěřil, až když si nechal zrentgenovat ruku), rádio považoval za zbytečný vynález, který nemá budoucnost, a také se domníval, že stroje těžší než vzduch, nikdy nebudou moc létat. Spolu s Albertem Michelsonem také zastával názor, že „ve fyzice už bylo všechno objeveno a jediné co teď zbývá, je už jen zpřesňovat výpočty.)
Během druhé světové války se německý astronom Walter Baade (v roce 1931 emigroval do USA) rozhodl ověřit Hubbleovo výpočty a skutečně se zdály být v pořádku. Jelikož tehdy bylo nařízeno zatemnění Los Angeles, měl Baade nejlepší pozorovací podmínky za několik posledních desítek let. Baadeho snažení ale nebylo zpočátku tak jednoduché. Přestože žil v USA již deset let, pro vládu to byl občan nepřátelského státu, a tak měl mezi západem Slunce a svítáním zákaz vycházet z domu, což je pro astronoma asi stejný problém jako kdybyste hokejistovi zakázali používat hokejku. Nakonec Baade dostal výjimku a mohl tak nerušeně pokračovat v práci. Pro kalibraci si vybral proměnné hvězdy typu RR Lyrae, které se dosud používali jen k měření v rámci naší Galaxie. Z grafu lze vyčíst proč. RR Lyrae mají kratší periodu (4 až 30 hodin) než obyčejné cefeidy a také mají mnohem nižší absolutní magnitudu. Většina cefeid má zářivý výkon v řádech tisíců či desetitisíců Sluncí, kdežto zářivost RR Lyrae se pohybuje mezi 40 až 50 Slunci - to znamená, že příliš vzdálené RR Lyrae už nelze pozorovat, neboť jsou zkrátka málo jasné. Podle výpočtů by ale přesto měly být v Andromedě vidět. Baade je pozoroval (nebo se spíše snažil je pozorovat) několik týdnů, ale nenašel po nich ani stopu. To vedlo ke třem závěrům: buďto měl prostě smůlu, když RR Lyrae nenašel, nebo se v Andromedě žádné RR Lyrae nevyskytují, anebo se Andromeda nachází dál, než jsme si mysleli. Jak asi správně tušíte, cé je správně. Andromeda se podobá naší Galaxii, takže když v naší Galaxii RR Lyrae jsou, tak není žádný důvod se domnívat, že by v Andromedě být neměly.
Baade zjistil, že cefeidy v Andromedě patří k mladší populaci I, zatímco ty naše jsou staršího typu II. Hvězdy v Andromedě jsou tedy 4x zářivější (2,51,5 = 4), a proto se Andromeda musí nacházet ve dvojnásobné vzdálenosti, než se doposud myslelo. Baade tak upravil její vzdálenost na cca 2,3 milionu světelných let (podle posledních studií se tato vzdálenost dokonce ještě trochu navýšila - dnes se udává hodnota kolem 2,5 až tří miliónů světelných let). Protože ostatní vesmírné vzdálenosti se určovaly na základě této vzdálenosti, dalo by se tak říci, že vesmír se najednou ze dne na den dvakrát zvětšil.
To je ovšem v rozporu s mými výpočty. Podle nich se totiž Andromeda nachází jen pár metrů od mého gauče:

Stejně jako předchozí metody, i proměnné hvězdy mají svůj vzdálenostní limit. Cefeidy můžeme využít na vzdálenost až sto miliónů světelných let, hvězdy RR Lyrae pak "jen" do 2,5 milionu. Mohlo by se tak zdát, že RR Lyrae nemají větší uplatnění, ale opak je pravdou. Jejich pravidelná pulsace je umožňuje velice snadno identifikovat. Největší roli sehrály při stanovování vzdáleností hvězdokup. Hvězdokupy jsou shluky hvězd, které vznikají společně ze stejného oblaku prachu a plynu. Z tohoto důvodu je jejich složení, vzdálenost i stáří skoro stejné, čehož lze dobře využít pro porovnávání vzdáleností mezi dalšími hvězdokupami.
Vzdálené galaxie
Cefeidy nejsou jedinými standardními svíčkami vesmíru. Dalším typem jsou supernovy typu Ia (nikoli jako oslovské iá, ale jedna á). Jak už jsme si stručně řekli v kapitole o vývoji hvězd, některé hvězdy končí svůj vesmírný život gigantickým výbuchem, který svým jasem hravě přezáří celé galaxie. (Nakonec z takových hvězd vznikne černá díra nebo rychle rotující neutronová hvězda - pulsar.) V naší Galaxii explodují každých sto let přibližně dvě až tři takové supernovy. Všechny Ia mají přibližně stejnou hmotnost, a proto se při jejich výbuchu uvolňuje stejné množství energie i jasu (jedná se o energii asi 100 až 200 triliard triliard joulů, to je docela dost velké číslo, v nezkráceném zápisu vypadá asi takto: 100 až 200 000 000 000 000 000 000 000 000 000 000 000 000 000 000 J). Pokud tedy známe absolutní jasnost a porovnáme ji se zdánlivou, pak můžeme snadno dopočítat vzdálenost. Po explozi je většina hmoty vyvržena do okolí ve formě jakési obálky, ta má rychlost 10 000 km/s a postupem času se neustále zvětšuje - tím roste i její absolutní jasnost. Během několika prvních dní tato obálka natolik zvětší svoji plochu, že absolutní jasnost  dosáhne maxima. Ta je u všech supernov typu Ia stejně velké, asi -19,3 magnitudy. Několik dalších týdnů se pak obálka ochlazuje, až se zcela ztratí z dohledu. Supernovy Ia jsou tak asi 300 000x zářivější než cefeidy. Z toho vyplývá, že je můžeme pozorovat na pětisetnásobnou vzdálenost, tedy asi na vzdálenosti pěti miliard světelných let!
dosáhne maxima. Ta je u všech supernov typu Ia stejně velké, asi -19,3 magnitudy. Několik dalších týdnů se pak obálka ochlazuje, až se zcela ztratí z dohledu. Supernovy Ia jsou tak asi 300 000x zářivější než cefeidy. Z toho vyplývá, že je můžeme pozorovat na pětisetnásobnou vzdálenost, tedy asi na vzdálenosti pěti miliard světelných let!
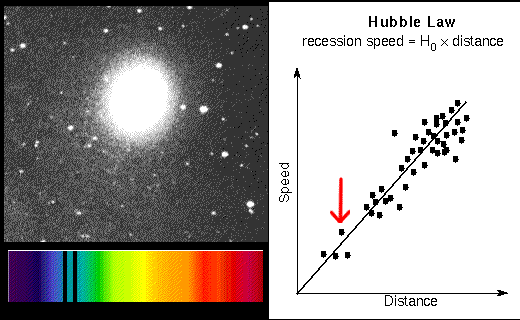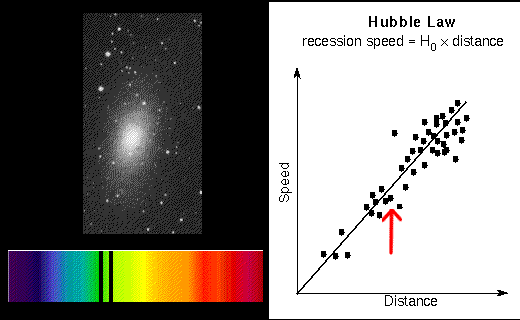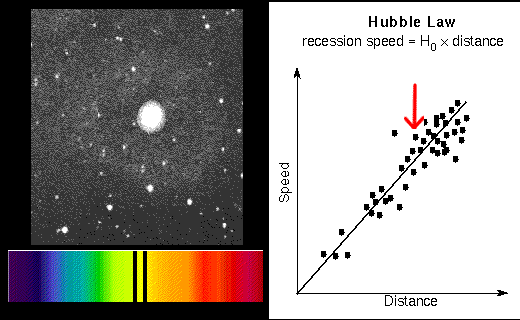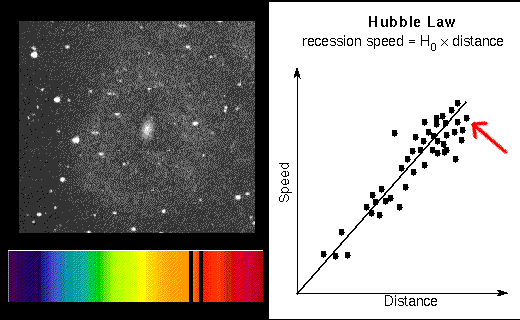
Další způsob zjišťování intergalaktických vzdáleností vychází z faktu, že se vesmír rozpíná. Ve stejné kapitole jsme si i řekli, že rychlost vzdalování galaxií je přímo úměrná jejich vzdálenosti. Čím dál se od nás nějaká galaxie nachází, tím rychleji se od nás vzdaluje. Můžeme to vyjádřit vzorcem v = d·H, kde v je rychlost, d je vzdálenost a H je Hubbleova konstanta  (cca 240 000 km·s-1·ly-1). Každá galaxie vyzařuje v nějakém spektru. Tím, že se pohybuje, dochází k určitému posuvu, který můžete vidět na vedlejším obrázku. Galaxie, která by vůči nám byla v klidu, by vyzařovala podle horního spektra. Další dvě spektra jsou stejná, ale spektrální čáry chemických prvků jsou posunuty. Jelikož modré vlny mají větší frekvenci, jsou spektrální čáry posunuty směrem doleva. Červené vlny jsou delší, a proto dochází k posuvu směrem doprava - tomuto jevu se říká rudý posuv. Jestliže λs bude skutečná vlnová délka, a λn naměřená, pak můžeme vyjádřit jejich poměr jako λp = λn / λs. Protože poměr rychlosti vzdalování k rychlosti světla (v/c) je stejný jako poměr posunutí vln (λp = λn/λs), pak můžeme dosadit do původní rovnice a zjistit, že vzdálenost d = (c/H)·λp. Platí tedy, že čím větší rudý posuv naměříme, tím je od nás galaxie vzdálenější.
(cca 240 000 km·s-1·ly-1). Každá galaxie vyzařuje v nějakém spektru. Tím, že se pohybuje, dochází k určitému posuvu, který můžete vidět na vedlejším obrázku. Galaxie, která by vůči nám byla v klidu, by vyzařovala podle horního spektra. Další dvě spektra jsou stejná, ale spektrální čáry chemických prvků jsou posunuty. Jelikož modré vlny mají větší frekvenci, jsou spektrální čáry posunuty směrem doleva. Červené vlny jsou delší, a proto dochází k posuvu směrem doprava - tomuto jevu se říká rudý posuv. Jestliže λs bude skutečná vlnová délka, a λn naměřená, pak můžeme vyjádřit jejich poměr jako λp = λn / λs. Protože poměr rychlosti vzdalování k rychlosti světla (v/c) je stejný jako poměr posunutí vln (λp = λn/λs), pak můžeme dosadit do původní rovnice a zjistit, že vzdálenost d = (c/H)·λp. Platí tedy, že čím větší rudý posuv naměříme, tím je od nás galaxie vzdálenější.
Závěr
Od prostého pozorování oblohy, kdy jsme změřili celou Sluneční soustavu, jsme se dostali k hvězdným paralaxám. Vzdálenosti blízkých hvězd zpočátku nebyly příliš důvěryhodné, ale s vypuštěním družice Hipparcos se přesnost rapidně zvýšila. Poté nastalo období fotometrie a spektroskopie (porovnávání zdánlivých a absolutních jasností), kdy jsme již byli schopni odhadnout vzdálenosti nejen v naší, ale i v těch nejbližších galaxiích. Přesnost fotometrické i spektroskopické paralaxy se však nemůže rovnat trigonometrické paralaxe, proto se současně zavádí i jiné metody, které ověřují, nakolik zjištěná vzdálenost odpovídá skutečnosti. (Jako kalibrace může sloužit například rozbor tempa poklesu jasnosti nov, či tzv. metoda nejjasnějších hvězd, která tvrdí, že když najdete nejjasnější hvězdokupu v některé galaxii, a porovnáte ji s nejjasnější hvězdokupou v jiné galaxii, tak obě budou mít pravděpodobně stejnou zářivost.) Tento úkol je o to obtížnější, že velmi vzdálené hvězdy už vůbec nevidíme, a jediným způsob jak je pozorovat, je mimo viditelné spektrum. (K tomu se navíc připojují i další limitující faktory jako například mezihvězdný plyn a prach.) Na ty nejvzdálenější objekty pak využíváme supernovy (narozdíl od klasických standardních svíček mají nevýhodu, že si je nemůžeme zaměřit kdy chceme, ale musíme čekat, až se laskavě uráčí bouchnout), měření rudého posuvu (Hubbleovo zákon), anebo Tullyho-Fisherův vztah (svítivost spirálních galaxií je závislá na rychlosti jejich rotace.)
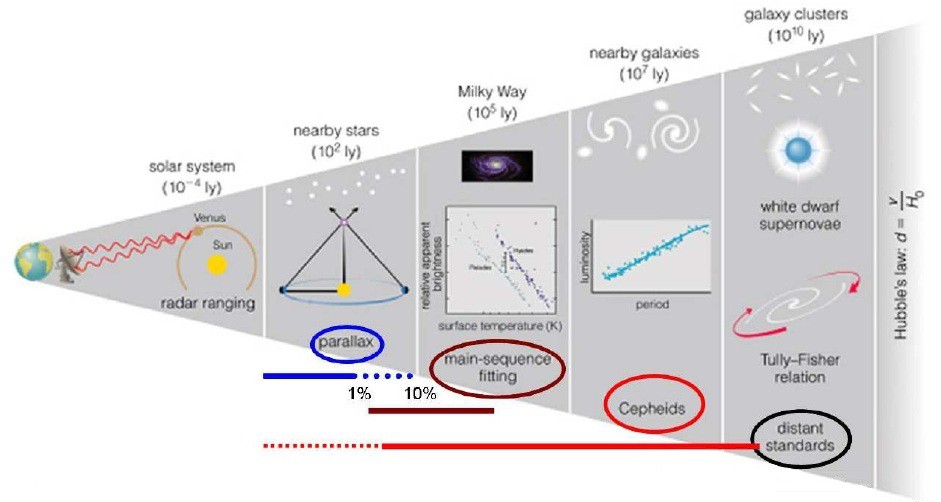
Stanovování vzdáleností ve vesmíru není jednoduchá věc, protože čím dále se díváme, tím obtížněji a méně přesně měříme. S každou další pomyslnou příčkou se chyba měření zvětšuje, neboť veškeré další odhady vyplývají již z dříve zjištěných vzdáleností. Jelikož každý náš krok je závislý na tom předchozím, bývá tento princip někdy označován jako kosmologický žebřík. Zatímco jeho základy jsou poměrně přesné a pevné, horní příčky se nejistě viklají. Nám už teď nezbývá nic jiného, než je zpevňovat...