E = mc²

Nejslavnější rovnice vědy dala základ jaderné energetice, ale také atomové bombě. Když tehdy Einstein viděl výsledek své práce, tak poznamenal: „Kdybych to byl býval věděl, raději bych se vyučil hodinářem.“ Co tato rovnice vlastně říká? Že množství energie ve hmotě je přímo úměrné její hmotnosti a čtverci rychlosti světla. Jelikož rychlost světla je  velké číslo (a co teprve jeho druhá mocnina!), tak můžeme říct, že i v nepatrném kousíčku hmoty se skrývá obrovské množství energie. Když si podle tohoto vzorce spočítáte energii ukrytou v 1 kg hmoty, vyjde vám 9·10¹⁶ J! To je dost energie na to, abyste  jednou čajovou lžičkou hmoty vyhodili do vzduchu váš dům a ještě přitom zorali sousedům zahrádku.

Pokud jste četli předchozí kapitolu, pak víte že, každé těleso, které urychlujeme, se stává těžší, protože energie, kterou mu dodáváme, se projevuje jako přírustek hmotnosti. Z toho tedy vyplývá, že energie má odpovídající hmotnost, musí tedy něco vážit!

Jestliže je teplo je mikroskopický pohyb, pak platí, že čím vyšší je teplota, tak tím rychleji se atomy pohybují. Naopak čím nižší teplota, tím je pohyb pomalejší. Atomy v plynu volně poletují sem a tam, zatímco v pevné látce či kapalině kmitají. Pokud bychom tedy byli schopni (zatím se to ještě nikomu nepovedlo) ochladit nějakou látku na absolutní nulu (0 Kelvinů = -273,15 stupňů Celsia), pak by ustal všechen pohyb - atomy by „zamrzly“. Tím se dostáváme k dalšímu vysvětlení, které jste si mohli na úvodní stránce přečíst, a to, proč šálek horké kávy váží víc než studený. Atomy v hrnku horké kávy kmitají mnohem rychleji než atomy v hrnku studené kávy, mají tedy větší pohybovou energii, a proto horká káva váží víc než studená. (Pokud se právě chystáte uvařit kávu a postavit jí na váhu, tak vám ušetřím čas - rozdíl tam sice je, ale pochopitelně je téměř neměřitelný.)

Díky vzorci E = mc² tedy víme, že energie něco váží. Hvězda, která nám dává život, Slunce, je ohromná zásobárna energie. Vyzáří do vesmíru tolik energie, že každou sekundu ztratí 4 miliony tun své hmotnosti! Možná to zní neuvěřitelně, ale Slunce je velké. Oproti nám je doslova gigantické – Zeměkoule by se do něj vešla více než milionkrát! Pro srovnání se podívejte na následující obrázky.

První ukazuje porovnání velikosti planet Sluneční soustavy (včetně Pluta, které, jak jistě víte, od roku 2006 není planetou):

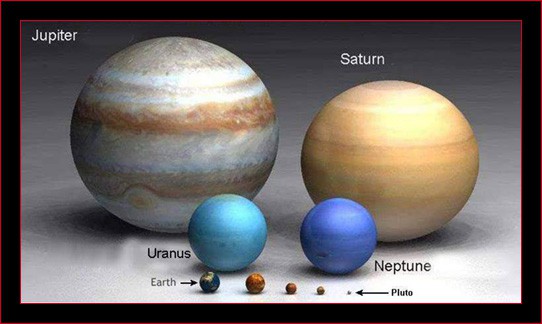
 A na dalším obrázku si můžete prohlédnout srovnání velikosti planet se Sluncem:

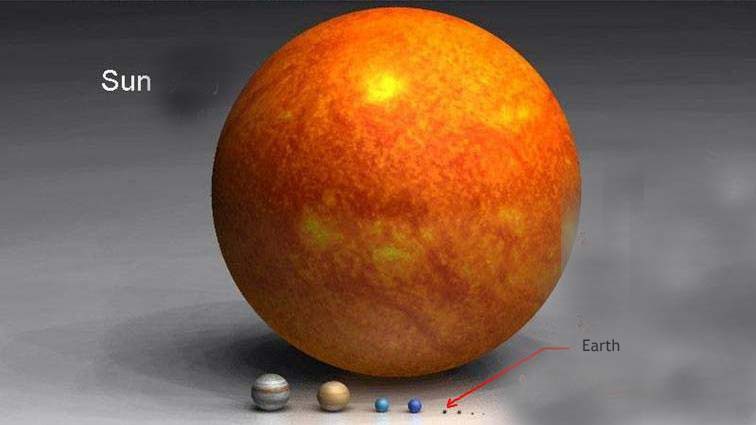
Teď je asi jasné, proč Slunce svou gravitací ovlivňuje celou naší soustavu

Touto rovnicí se dá vysvětlit i jev, který podrobněji proberu v kapitole o atomech. Jde o to, že hmotnost jádra atomu je menší než součet hmotností částic, z nichž se jádro skládá. Zatím nebudu předbíhat, takže jen pro pořádek uvedu, že tento hmotnostní úbytek odpovídá energii vazebných sil mezi částicemi a určuje energii, kterou bychom museli vynaložit, abychom jednotlivé částice od sebe oddálili. Existují ale atomy, které se rozpadají sami od sebe. Když se takový atom rozpadne, vzniknou nové částice. Součet hmotností takto nově vzniklých částic je přitom menší než hmotnost původního atomu. Jádra těžkých atomů, jako je například radium, jsou hodně velká, a tudíž i nestabilní. Například takové radium 226 obsahuje 88 protonů a 138 neutronů a samovolně se rozpadá na menší radon 222, který má 86 protonů a 136 neutronů. Chybějící dva protony a dva neutrony jsou pak vyvrženy v podobě alfa částice, kterou v tomto případě tvoří hélium 4. Při štěpení dojde k úbytku hmotnosti, například 1 kg radia se přemění na 0,999977 kg rad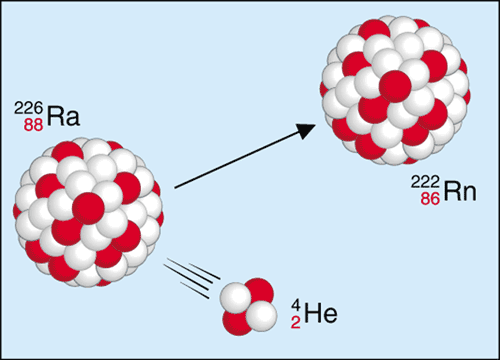onu a alfa částic. Pokud těch chybějících 0,000023 kg vynásobíte c², dostanete energii přes 2 biliony joulů. 1 kg trinitrotoluenu uvolní energii cca 4,2 megajoulů, takže v těch nepatrných 0,023 gramu je obsaženo téměř 500 tun TNT! Při jaderné fúzi (slučování atomů) se energie uvolňuje stejným způsobem, ale její množství je ještě o něco větší. Proto jsou vodíkové bomby využívající fůzi ničivější než plutoniové bomby, které využívají štěpení. Stejným způsobem se dají vysvětlit i ty čtyři miliony tun, které Slunce ztrácí každou sekundu - během ní se totiž mění 600 miliónů tun vodíku na 596 miliónů tun hélia.

Jen pro snaživce:

Na začátku jsem slíbil, že zde neuvidíte žádnou matematiku, proto tento odstaveček klidně můžete přeskočit. Dozvíte se tu pouze jednu jedinou věc, a to odvození E=mc².

V jedné knize jsem si přečetl, že tato slavná rovnice, která se stala jakýmsi synonymem pro vědu, jde odvodit na pár řádcích. Rozhodl jsem se, že to zkusím - otevřel jsem tedy starou dobrou Wikipedii a v domnění, že jí za pět minut zvládnu spočítat, jsem se do toho pustil. Bohužel v době, kdy jsem psal tyto stránky, byla teta Wiki poněkud líná a spousta věcí vynechala, takže následující postup je jakýsi mix mých poznámek a postupů s tím, co tehdy bylo na Wiki, a co si zde vlastně můžete přečíst i teď.

Propadal Einstein z matematiky? A je vůbec zápis E = mc² správně?

Možná jste slyšeli o tom, že Einstein na škole propadal z matematiky i fyziky. Ve skutečnosti tomu bylo přesně naopak, v obojím neobvykle vynikal. Tento mýtus zřejmě vznikl, když v Německu probíhala reforma školství a došlo ke změně známkování (asi jako kdyby se u nás najednou začali místo jedniček dávat pětky). Když Einstein dělal přijímací zkoušky na curyšskou polytechniku, propadl ze všech předmětů, kromě fyziky a matematiky. Dokonce v nich dosáhl tak výborných výsledků, že mu byla udělena výjimka a nakonec byl přijat. Přestože Einstein dobře ovládal matematiku, byl to především fyzik, a tak vás možná překvapí, že rovnice E = mc² není ve skutečnosti zcela správně. Podívejte se na operaci s odmocninami a představte si, že máte neznámou, označme ji třeba x, a ta se rovná odmocnině ze čtyř. Vaše odpověď asi bude znít, že x je rovno dvěma. To je ale pouze jedno řešení. Může to být i mínus dvě, takže správný zápis by měl být E = ±mc².

Dodatečné znaménko mínus se dá vysvětlit existencí antihmoty. Každá částice má svůj protějšek, který má stejnou hmotnost, ale ostatní charakteristiky mají opačné znaménko (například antičásticemi elektronu, neutronu a protonu jsou pozitron, antiproton a antineutron). V tuto chvíli nás nějaká antihmota nemusí vůbec zajímat, nicméně až budete číst kapitolu o Velkém třesku a černých dírách, bylo by dobré o ní něco vědět. Jak už jste si asi všimli, náš vesmír se evidentně skládá pouze z hmoty, tak si možná kladete otázku: "Kam se, sakra, poděla ta antihmota?" Pokud se srazí hmota s antihmotou, dojde k anihilaci - částice i antičástice zcela zaniknou a hmota se tak přemění v energii (vznikou též další typy částic a antičástic). (Stephen Hawking dokonce varoval, že kdybyste náhodou potkali svého antipartnera, tak mu raději nepodávejte ruku, protože byste okamžitě oba zanikly.) Na počátku vesmíru existovalo přibližně stejné množství hmoty a antihmoty, které se navzájem neustále sráželo. Protože ale nic není dokonalé, tak hmoty bylo ve skutečnosti trošku více než antihmoty, a to vedlo k tomu, že antihmota zkrátka zanikla a zbyla jen hmota, která tvoří vše kolem nás - od stromů, planet až ke galaxiím.

Tip pro podnikatele:

Pokud čirou náhodou máte po ruce pár miliard dolarů, můžete začít vyrábět antihmotu. V roce 2004 se CERNu podařilo vyrobit téměř biliontinu gramu antihmoty. Celá tato sranda stála asi 20 milionů dolarů, což z antihmoty dělá jednoznačně nejvzácnější látku na světě - výroba jednoho gramu by stála kolem 100 trilionů dolarů!  A co si s takovou drahou hračkou vlastně počít, když ji ani nemůžete nacpat do plechovky ani šoupnout do skladu? (Při kontaktu s obyčejnou hmotou by okamžitě došlo k anihilaci, a proto se antihmota musí "skladovat" ve vakuu pomocí silného elektromagnetického pole.) Energie, která vzniká při srážce antihmoty s hmotou, je vlastně nejenergičnější možnou reakcí v tomto vesmíru a může být využita v elektrárnách nebo jako pohon mezigalaktických lodí. (V rámci Sluneční soustavy by nám podle vzorce E = mc² stačilo jen pár gramů!) Má to ovšem jeden háček - kdybychom vzali hmotu a anihilovali jí s veškerou antihmotou, kterou se zatím kdy podařilo vyrobit, vznikla by energie, která by dokázala (a teď se držte...) rozsvítit obyčejnou žárovku a to na dobu několika málo minut!